

But when you count on data for building strategies, simplifying processes, and improving customer experience, more than collecting it, you need to understand and analyze it to be able to draw valuable insights. Analyzing data helps you study what’s already happened and predict what may happen in the future.
Data analysis has many components, and while some can be easy to understand and perform, others are rather complex. The good news is that many statistical analysis software offer meaningful insights from data in a few steps.
You have to understand the fundamentals before using or relying on a statistical program to give accurate results because even though generating results is easy, interpreting them is another ballgame.
While interpreting data, considering the factors that affect the data becomes essential. Regression analysis helps you do just that. With the assistance of this statistical analysis method , you can find the most important and least important factors in any data set and understand how they relate.
This guide covers the fundamentals of regression analysis, its process, benefits, and applications.
Regression analysis is a statistical process that helps assess the relationships between a dependent variable and one or more independent variables.
The primary purpose of regression analysis is to describe the relationship between variables, but it can also be used to:
To understand regression analysis comprehensively, you must build foundational knowledge of the statistical concepts.
Regression analysis helps identify the factors that impact data insights. You can use it to understand which factors play a role in creating an outcome and how significant they are. These factors are called variables.
You need to grasp two main types of variables.
Causation indicates that one variable is the result of the occurrence of the other variable. Correlation suggests a connection between variables. Correlation and causation can coexist, but correlation does not imply causation.
Overfitting is a statistical modeling error that occurs when a function lines up with a limited set of data points and makes predictions based on those instead of exploring new data points. As a result, the model can only be used as a reference to its initial data set and not to any other data sets.
For a minute, let's imagine that you own an ice cream stand. In this case, we can consider “revenue” and “temperature” to be the two factors under analysis. The first step toward conducting a successful regression statistical analysis is gathering data on the variables.
You collect all your monthly sales numbers for the past two years and any data on the independent variables or explanatory variables you’re analyzing. In this case, it’s the average monthly temperature for the past two years.
To begin to understand whether there’s a relationship between these two variables, you need to plot these data points on a graph that looks like the following theoretical example of a scatter plot:
.png?width=600)
The amount of sales is represented on the y-axis (vertical axis), and temperature is represented on the x-axis (horizontal axis). The dots represent one month's data – the average temperature and sales in that same month.
Observing this data shows that sales are higher on days when the temperature increases. But by how much? If the temperature goes higher, how much do you sell? And what if the temperature drops?
Drawing a regression line roughly in the middle of all the data points helps you figure out how much you typically sell when it’s a specific temperature. Let’s use a theoretical scatter plot to depict a regression line:
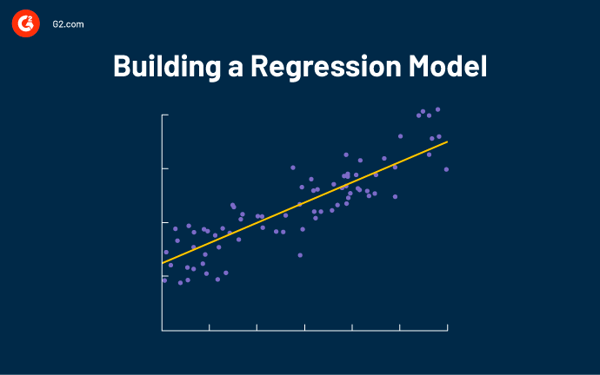
The regression line explains the relationship between the predicted values and dependent variables. It can be created using statistical analysis software or Microsoft Excel.
Your regression analysis tool must also display a formula that defines the slope of the line. For example:
y = 100 + 2x + error term
On observing the formula, you can conclude that when there is no x, y equals 100, which means that when the temperature is very low, you can make an average of 100 sales. Provided the other variables remain constant, you can use this to predict the future of sales. For every rise in the temperature, you make an average of two more sales.
A regression line always has an error term because an independent variable cannot be a perfect predictor of a dependent variable. Deciding whether this variable is worth your attention depends on the error term – the larger the error term, the less certain the regression line.
Various types of regression analysis are at your disposal, but the five mentioned below are the most commonly used.
A linear regression model is defined as a straight line that attempts to predict the relationship between variables. It’s mainly classified into two types: simple and multiple linear regression.
We’ll discuss those in a moment, but let’s first cover the five fundamental assumptions made in the linear regression model.
Linear regression analysis helps predict a variable's value (dependent variable) based on the known value of one other variable (independent variable).
Linear regression fits a straight line, so a simple linear model attempts to define the relationship between two variables by estimating the coefficients of the linear equation.
Where,
Y – Dependent variable (response variable)
X – Independent variable (predictor variable)
a – Intercept (y-intercept)
b – Slope
ϵ – Residual (error)
I n such a linear regression model, a response variable has a single corresponding predictor variable that impacts its value. For example, consider the linear regression formula:
y = 5x + 4
If the value of x is defined as 3, only one possible outcome of y is possible.
In most cases, simple linear regression analysis can't explain the connections between data. As the connection becomes more complex, the relationship between data is better explained using more than one variable.
Multiple regression analysis describes a response variable using more than one predictor variable. It is used when a strong correlation between each independent variable has the ability to affect the dependent variable.
Y = a + bX1 + cX2 + dX3 + ϵ
Where,
Y – Dependent variable
X1, X2, X3 – Independent variables
a – Intercept (y-intercept)
b, c, d – Slopes
ϵ – Residual (error)
Ordinary Least Squares regression estimates the unknown parameters in a model. It estimates the coefficients of a linear regression equation by minimizing the sum of the squared errors between the actual and predicted values configured as a straight line.
A linear regression algorithm only works when the relationship between the data is linear. What if the data distribution was more complex, as shown in the figure below?
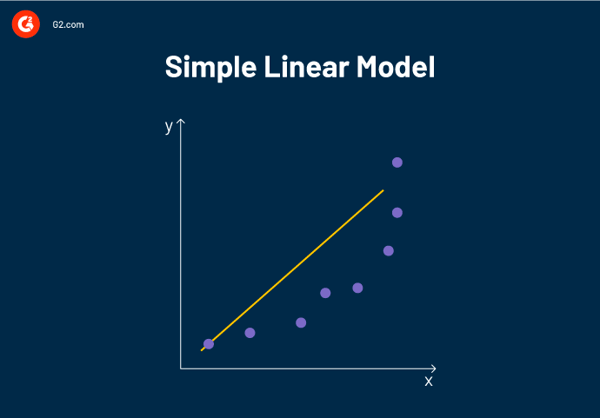
As seen above, the data is nonlinear. A linear model can't be used to fit nonlinear data because it can't sufficiently define the patterns in the data.
Polynomial regression is a type of multiple linear regression used when data points are present in a nonlinear manner. It can determine the curvilinear relationship between independent and dependent variables having a nonlinear relationship.
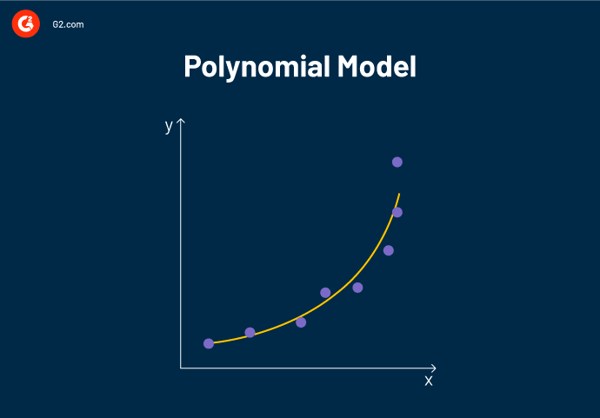
y = b0+b1x1+ b2x1^2+ b2x1^3+. bnx1^n
Logistic regression models the probability of a dependent variable as a function of independent variables. The values of a dependent variable can take one of a limited set of binary values (0 and 1) since the outcome is a probability.
Logistic regression is often used when binary data (yes or no; pass or fail) needs to be analyzed. In other words, using the logistic regression method to analyze your data is recommended if your dependent variable can have either one of two binary values.
Let’s say you need to determine whether an email is spam. We need to set up a threshold based on which the classification can be done. Using logistic regression here makes sense as the outcome is strictly bound to 0 (spam) or 1 (not spam) values.
In other regression methods, the output is derived from one or more attributes. But what if those attributes are unavailable?
The bayesian regression method is used when the dataset that needs to be analyzed has less or poorly distributed data because its output is derived from a probability distribution instead of point estimates. When data is absent, you can place a prior on the regression coefficients to substitute the data. As we add more data points, the accuracy of the regression model improves.
Imagine a company launches a new product and wants to predict its sales. Due to the lack of available data, we can’t use a simple regression analysis model. But Bayesian regression analysis lets you set up a prior and calculate future projections.
Additionally, once new data from the new product sales come in, the prior is immediately updated. As a result, the forecast for the future is influenced by the latest and previous data.
The Bayesian technique is mathematically robust. Because of this, it doesn’t require you to have any prior knowledge of the dataset during usage. However, its complexity means it takes time to draw inferences from the model, and using it doesn't make sense when you have too much data.
The linear regression method estimates a variable's mean based on the values of other predictor variables. But we don’t always need to calculate the conditional mean. In most situations, we only need the median, the 0.25 quantile, and so on. In cases like this, we can use quantile regression.
Quantile regression defines the relationship between one or more predictor variables and specific percentiles or quantiles of a response variable. It resists the influence of outlying observations. No assumptions about the distribution of the dependent variable are made in quantile regression, so you can use it when linear regression doesn’t satisfy its assumptions.
Let's consider two students who have taken an Olympiad exam open for all age groups. Student A scored 650, while student B scored 425. This data shows that student A has performed better than student B.
But quantile regression helps remind us that since the exam was open for all age groups, we have to factor in r the student's age to determine the correct outcome in their individual conditional quantile spaces.
We know the variable causing such a difference in the data distribution. As a result, the scores of the students are compared for the same age groups.
Regularization is a technique that prevents a regression model from overfitting by including extra information. It’s implemented by adding a penalty term to the data model. It allows you to keep the same number of features by reducing the magnitude of the variables. It reduces the magnitude of the coefficient of features toward zero.
The two types of regularization techniques are L1 and L2. A regression model using the L1 regularization technique is known as Lasso regression, and the one using the L2 regularization technique is called Ridge regression.
Ridge regression is a regularization technique you would use to eliminate the correlations between independent variables (multicollinearity) or when the number of independent variables in a set exceeds the number of observations.
Ridge regression performs L2 regularization. In such a regularization, the formula used to make predictions is the same for ordinary least squares, but a penalty is added to the square of the magnitude of regression coefficients. This is done so that each feature has as little effect on the outcome as possible.
Lasso stands for Least Absolute Shrinkage and Selection Operator.
Lasso regression is a regularized linear regression that uses an L1 penalty that pushes some regression coefficient values to become closer to zero. By setting features to zero, it automatically chooses the required feature and avoids overfitting.
So if the dataset has high correlation, high levels of multicollinearity, or when specific features such as variable selection or parameter elimination need to be automated, you can use lasso regression.
Now is the time to get SaaS-y news and entertainment with our 5-minute newsletter, G2 Tea , featuring inspiring leaders, hot takes, and bold predictions. Subscribe today!

Regression analysis is a powerful tool used to derive statistical inferences for the future using observations from the past . It identifies the connections between variables occurring in a dataset and determines the magnitude of these associations and their significance on outcomes.
Across industries, it’s a useful statistical analysis tool because it provides exceptional flexibility. So the next time someone at work proposes a plan that depends on multiple factors, perform a regression analysis to predict an accurate outcome.
In the real world, various factors determine how a business grows. Often these factors are interrelated, and a change in one can positively or negatively affect the other.
Using regression analysis to judge how changing variables will affect your business has two primary benefits.
Both small and large industries are loaded with an enormous amount of data. To make better decisions and eliminate guesswork, many are now adopting regression analysis because it offers a scientific approach to management.
Using regression analysis, professionals can observe and evaluate the relationship between various variables and subsequently predict this relationship's future characteristics.
Companies can utilize regression analysis in numerous forms. Some of them:
Businesses with a data-driven culture use regression analysis to draw actionable insights from large datasets. For many leading industries with extensive data catalogs, it proves to be a valuable asset. As the data size increases, further executives lean into regression analysis to make informed business decisions with statistical significance.
While Microsoft Excel remains a popular tool for conducting fundamental regression data analysis, many more advanced statistical tools today drive more accurate and faster results. Check out the top statistical analysis software in 2023 here.
To be included in this category, the regression analysis software product must be able to:
*Below are the top 5 leading statistical analysis software solutions from G2’s Winter 2023 Grid® Report. Some reviews may be edited for clarity.
IBM SPSS Statistics allows you to predict the outcomes and apply various nonlinear regression procedures that can be used for business and analysis projects where standard regression techniques are limiting or inappropriate. With IBM SPSS Statistics, you can specify multiple regression models in a single command to observe the correlation between independent and dependent variables and expand regression analysis capabilities on a dataset.
"I have used a couple of different statistical softwares. IBM SPSS is an amazing software, a one-stop shop for all statistics-related analysis. The graphical user interface is elegantly built for ease. I was quickly able to learn and use it"
"Some of the interfaces could be more intuitive. Thankfully much information is available from various sources online to help the user learn how to set up tests."
To make data science more intuitive and collaborative, Posit provides users across key industries with R and Python-based tools, enabling them to leverage powerful analytics and gather valuable insights.
"Straightforward syntax, excellent built-in functions, and powerful libraries for everything else. Building anything from simple mathematical functions to complicated machine learning models is a breeze."
"Its GUI could be more intuitive and user-friendly. One needs a lot of time to understand and implement it. Including a package manager would be a good idea, as it has become common in many modern IDEs. There must be an option to save console commands, which is currently unavailable."
JMP is a data analysis software that helps make sense of your data using cutting-edge and modern statistical methods. Its products are intuitively interactive, visually compelling, and statistically profound.
"The instructional videos on the website are great; I had no clue what I was doing before I watched them. The videos make the application very user-friendly."
"Help function can be brief in terms of what the functionality entails, and that's disappointing because the way the software is set up to communicate data visually and intuitively suggests the presence of a logical and explainable scientific thought process, including an explanation of the "why.” The graph builder could also use more intuitive means to change layout features."
Minitab Statistical Software is a data and statistical analysis tool used to help businesses understand their data and make better decisions. It allows companies to tap into the power of regression analysis by analyzing new and old data to discover trends, predict patterns, uncover hidden relationships between variables, and create stunning visualizations.
"The greatest program for learning and analyzing as it allows you to improve the settings with incredibly accurate graphs and regression charts. This platform allows you to analyze the outcomes or data with their ideal values."
"The software price is steep, and licensing is troublesome. You are required to be online or connected to the company VPN for licensing, especially for corporate use. So without an internet connection, you cannot use it at all. Also, if you are in the middle of doing an analysis and happen to lose your internet connection, you will risk losing the project or the study you are working on."
EViews offers user-friendly tools to perform data modeling and forecasting. It operates with an innovative, easy-to-use object-oriented interface used by researchers, financial institutions, government agencies, and educators.
"As an economist, this software is handy as it assists me in conducting advanced research, analyzing data, and interpreting results for policy recommendations. I just cannot do without EViews. I like its recent updates that have also enhanced the UI."
"In my experience, importing data from Excel is not easy using EViews compared to other statistical software. One needs to develop expertise while importing data into EViews from different formats. Moreover, the price of the software is very high."

Data collection has become easy in the modern world, but more than just gathering is required. Businesses must know how to get the most value from this data. Analysis helps companies to understand the available information, derive actionable insights, and make informed decisions. Businesses should thoroughly know the data analysis process inside and out to refine operations, improve customer service, and track performance.
Learn more ab out the various stages of data analysis and implement them to drive success.
Devyani Mehta is a content marketing specialist at G2. She has worked with several SaaS startups in India, which has helped her gain diverse industry experience. At G2, she shares her insights on complex cybersecurity concepts like web application firewalls, RASP, and SSPM. Outside work, she enjoys traveling, cafe hopping, and volunteering in the education sector. Connect with her on LinkedIn.