
Did you know that a conditional statement is also referred to as a logical implication?

Jenn, Founder Calcworkshop ® , 15+ Years Experience (Licensed & Certified Teacher)
Let’s dive into today’s discrete lesson and find out how this works.
A conditional statement represents an if…then statement where p is the hypothesis (antecedent), and q is the conclusion (consequent). In essence, it is a statement that claims that if one thing is true, then something else is true also.
Here are a few examples of conditional statements:
“If it is sunny, then we will go to the beach.”
“If the sky is clear, then we will be able to see the stars.”
“Studying for the test is a sufficient condition for passing the class.”
What is important to note is that the arrow that separates the hypothesis from the conclusion has countless translations.
Here’s a typical list of ways we can express a logical implication:
Notice that a conditional statement “if p then q” is false when p is true and q is false, and true otherwise as noted by Northern Illinois University.

Conditional Statement Truth Table
Now, another necessary type of implication is called a biconditional statement.
A biconditional statement, sometimes referred to as a bi-implication, may take one the following forms:
And the biconditional statement of “p if and only q” is true when p and q have the same truth values.
![]()
Biconditional Truth Table
Consequently, a biconditional statement can be expressed as a combination of two implications: p then q and q then p.
![]()
Biconditional Equivalence Tautology
Now that we’ve covered conditional and biconditional statements, it’s important to recognize that mastering these concepts is an essential part of learning discrete math. As we continue, you’ll see how these ideas build a foundation for more advanced topics and applications in discrete mathematics.
Additionally, we will discover six different types of sentences in propositional logic, and we will learn how to translate from English to symbols and vice versa with ease.

Symbolic Logic Statements
Furthermore, we will learn how to take conditional statements and find new compound statements in the converse, inverse, and contrapositive form.
It is imperative to note that order matters when determining the validity of a statement.
For example, let’s suppose we have the proposition: “If the card is a club, then it is black,” has a very different truth value than “if the card is black, then it is a club.”
The first conditional statement is true, that if we pull a club from a deck of cards, then that card will be black.
However, the second proposition would be false since a deck of cards has two black suites: clubs and spades — therefore, we are not necessarily guaranteed that pulling a black card will result in a club.
And being able to verify the truth value of conditional statements and its inverse, converse, and the contrapositive is going to be an essential part of our analysis.
But here’s a useful tip: the conditional statement and its contrapositive will always have the same truth value!
Consider the implication: if n is an odd integer, then 5n+1 is even. Write the converse, inverse, contrapositive, and biconditional statements.
More importantly, we will also discover how to determine the truth value for various implications using truth tables.
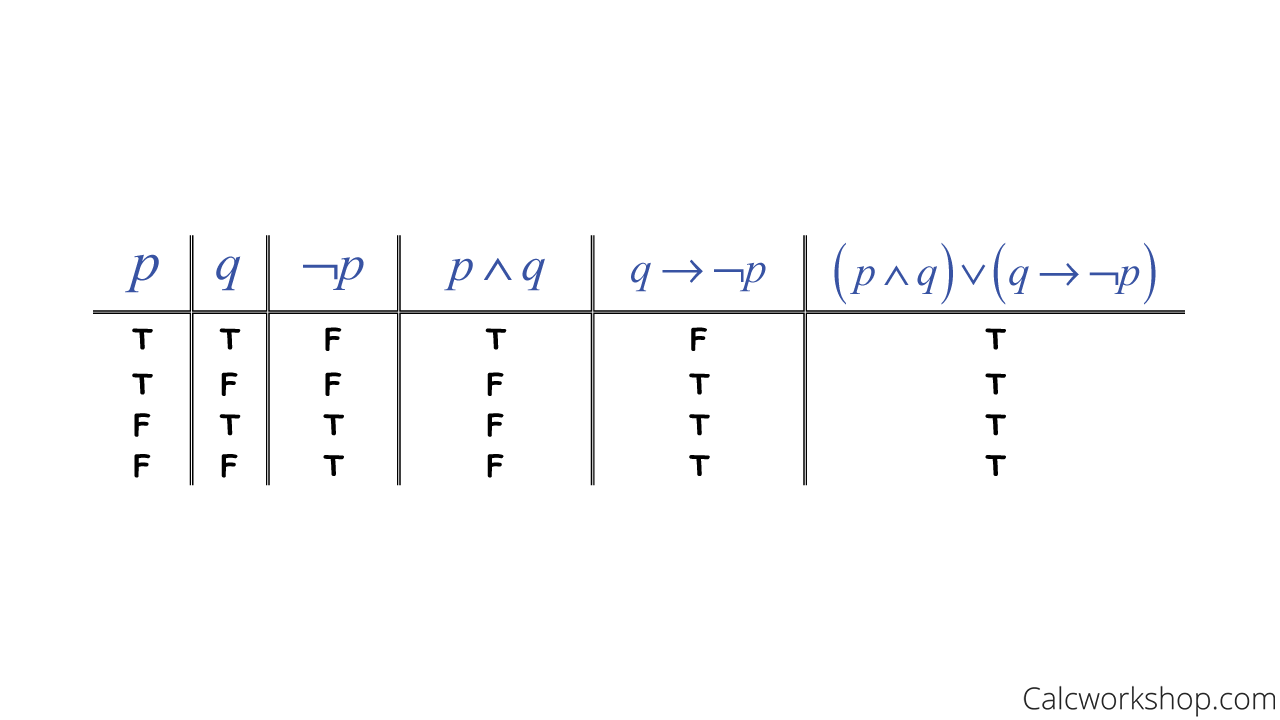
Conditional Truth Table
Together we will explore conditional statements and biconditional statements, as well as the converse, inverse, and contrapositive. Discovering how to translate words into symbols and symbols into words and verifying truth and falsehood for various implications using truth tables.
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.